Examen para casa de ESTADÍSTICA

Matemáticas Aplicadas a las Ciencias Sociales I

ESTADÍSTICA

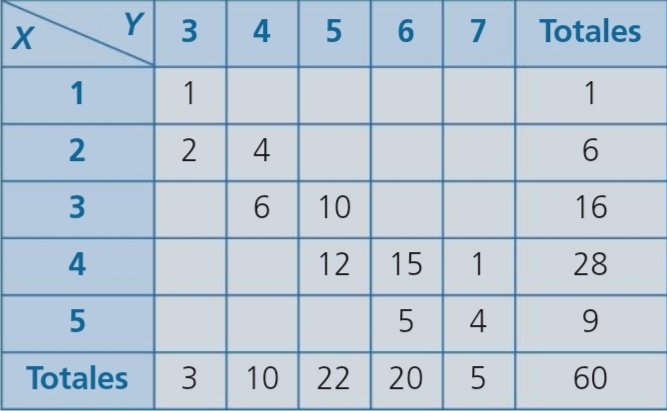
1.- Dibuja la nube de puntos y usa tu calculadora en modo estadístico para calcular la media y la desviación típica de las variables X e Y, la covarianza, el coeficiente de correlación lineal de Pearson y las dos rectas de regresión lineal y estima el valor de Y para X = 6.

2.- ¿Cuántos términos tiene un polinomio homogéneo en 3 indeterminadas de grado 3? Se elige, al azar, del conjunto de los polinomios en tres indeterminadas de grado 3 con coeficientes en A={0,1,2} un polinomio. ¿Cuál es la probabilidad de que sea homogéneo?

3.- ¿Cuántos sucesos aleatorios tiene el espacio de sucesos aleatorios de un experimento aleatorio cuyo espacio muestral tiene n sucesos elementales? Utiliza el binomio de Newton para razonar tu respuesta.

4.- Una urna contiene 3 bolas rojas, 3 bolas amarillas y 4 bolas verdes. Se extraen 2 bolas al azar, ¿cuál es la probabilidad de que una de esas bolas sea roja y la otra amarilla?

5.- Se colocan al azar los primeros n números naturales, 1, 2, 3,..., n en una línea. ¿Cuál es la probabilidad de que los números 2 y 3 estén seguidos en ese orden?

6.- Participar en el juego pagando una apuesta. Se realizan lanzamientos sucesivos de una moneda hasta que salga cruz por primera vez, se detiene el juego, se cuenta el número n de lanzamientos realizados, el jugador obtiene 2ⁿ euros. ¿Cuánto pagarías por jugar a este juego?

7.- El 9% de una población tiene cabello gris, el 5% tiene ojos grises y el 13% tiene cabello u ojos grises. Se elige una persona al azar, ¿cuál es la probabilidad de que su pelo y sus ojos no sean grises? Y si tiene pelo gris, ¿cuál es la probabilidad de que tenga ojos grises?

8.- Se eligen al azar 4 pasteles de entre pasteles de 6 tipos, ¿cuál es la probabilidad de que en mi selección haya 3 pasteles del mismo tipo?

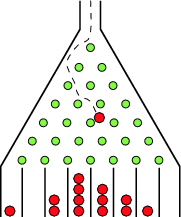
9.- Si soltamos una bola en la máquina de Galton con n filas de clavos, ¿cuál es la probabilidad de que caiga en cada uno de los contenedores de abajo?

10.- En un grupo de 100 personas hay 12 hombres fumadores y 67 mujeres no fumadoras. Elabora una tabla de contingencia y los diagramas de árbol. Se extrae al azar una persona de dicho grupo y resulta ser una mujer, ¿cuál es la probabilidad de que sea fumadora?

11.- Un concursante debe elegir una puerta entre tres. Tras una de ellas hay un coche y tras las otras hay una cabra. El concursante elige una y el presentador abre una de las dos en la que hay una cabra y le da la opción de cambiar. ¿Debe mantener su puerta o escoger la otra?

12.- Un avión cuatrimotor (dos motores en cada ala) no entra en emergencia mientras no fallen al menos un motor en cada ala. La probabilidad de que un motor cualquiera falle es 0,0001 de forma independiente. ¿Cuál es la probabilidad de que el avión entre en emergencia?

13.- ¿Qué es una función de densidad de probabilidad? Pon tres ejemplos.

14.- Sea X una variable aleatoria normal de media 25 y desviación típica 5, N(25,5). Halla

1. La probabilidad de que la variable X tome valores entre 14 y 28.
2. La probabilidad de que la variable X tome un valor mayor que 23.
3. La probabilidad de que la variable X tome un valor menor que 10.
4. La probabilidad de que la variable X tome un valor igual a 25.

15.- Las notas de cierto examen se distribuyen según una N(5’8,2’4), normal de media 5’8 y desviación típica 2’4. Halla la probabilidad de que la media aritmética de una muestra tomada al azar de 16 estudiantes esté comprendida entre 5 y 7 sabiendo que el estimador media muestral sigue una distribución normal  de esperanza matemática 5’8 y desviación típica .