El resto de una división entera

1. Con el algoritmo de la división entera
   
   Dividendo = divisor · cociente + resto                    resto < divisor
   
   55521        |__7_______
     65             7931
       22
         11
           4 <-- resto
   
   
2. Con la calculadora
   
   División decimal >> 55521 : 7 = 7931,5714285714285714285714285714... ¿Es periódico?
   Si el resultado es ENTERO entonces el resto es 0 (algunos libros lo llaman "división exacta"), y si no; al resultado le restamos la parte entera >>
   7931,5714285714285714285714285714 - 7931 = 0,57142857142857142857142857142857
   Y finalmente multiplicamos por el divisor, 7 >>
   0,57142857142857142857142857142857 · 7 = 4 <-- resto
   
   
3. Con el grafo de divisibilidad
   
   
   
   * ¿Cómo se crea?
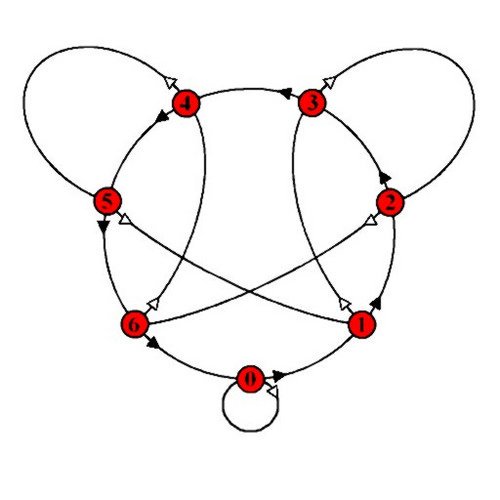
   Un grafo de divisibilidad es un grafo dirigido que tiene tantos vértices como restos posibles de la división entera. En nuestro caso (el divisor es 7): 0, 1, 2, 3, 4, 5 y 6. ¡Recuerda que el resto es menor que el divisor. Y las aristas son flechas y las hay de dos tipos: negras y blancas. Los vértices se colocan de manera ordenada (ver figura) y las flechas negras van de un vértice al siguiente y el último (6) va al primero (0). ¿Y cómo se dibujan las flechas blancas? De cada vértice sale una flecha blanca que va al vértice que se obtiene de la siguiente manera: se multiplica por 10 el número de dicho vértice y se halla el resto de la división entera por , en nuestro caso, 7; y la flecha blanca irá al vértice con dicho resto.
   
   * ¿Cómo se usa?
   Nos situamos en el vértice con el número 0 y cogemos las cifras de una en una y de izquierda a derecha del número propuesto. Por cada cifra, excepto la de las unidades, avanzamos por las flechas negras tantos vértices como indique la cifra e inmediatamente avanzamos por la flecha blanca. Con la cifra de las unidades hacemos lo mismo excepto que no usamos la flecha blanca. El vértice en el que terminemos nos indica el resto de dicha división entera.
   
   
   Ejercicios:
   * ¿511 es un número primo? ¿Qué es un número primo de Mersenne?
   n =1: 1 actualmente NO es primo.
   n =2: 3 primo.
   n =3: 7 primo.
   n =4: 15
   n =5: 31 primo.
   n =6: 63
   n =7: 127 primo.
   n =8: 255
   n =9: 511
   n =10: 1023
   n =11: 2047 >> Crea el grafo de divisibilidad del 23 y úsalo con 2047.
   ...
   * ¿Qué es una conjetura? Conjetura de Mersenne. Otras conjeturas famosas.
   * Lee el siguiente artículo de Miguel Ángel Morales Medina, autor del blog GAUSSIANOS, y utiliza el grafo de divisibilidad del 23 para hallar la letra de tu DNI >> El grafo adivinador de la letra del DNI