Martes 24 de marzo de 2020

Teorema de Pitágoras

Este teorema es muy conocido por los estudiantes ¿o no? Alguno lo recita de memoria sin entender muy bien su significado.

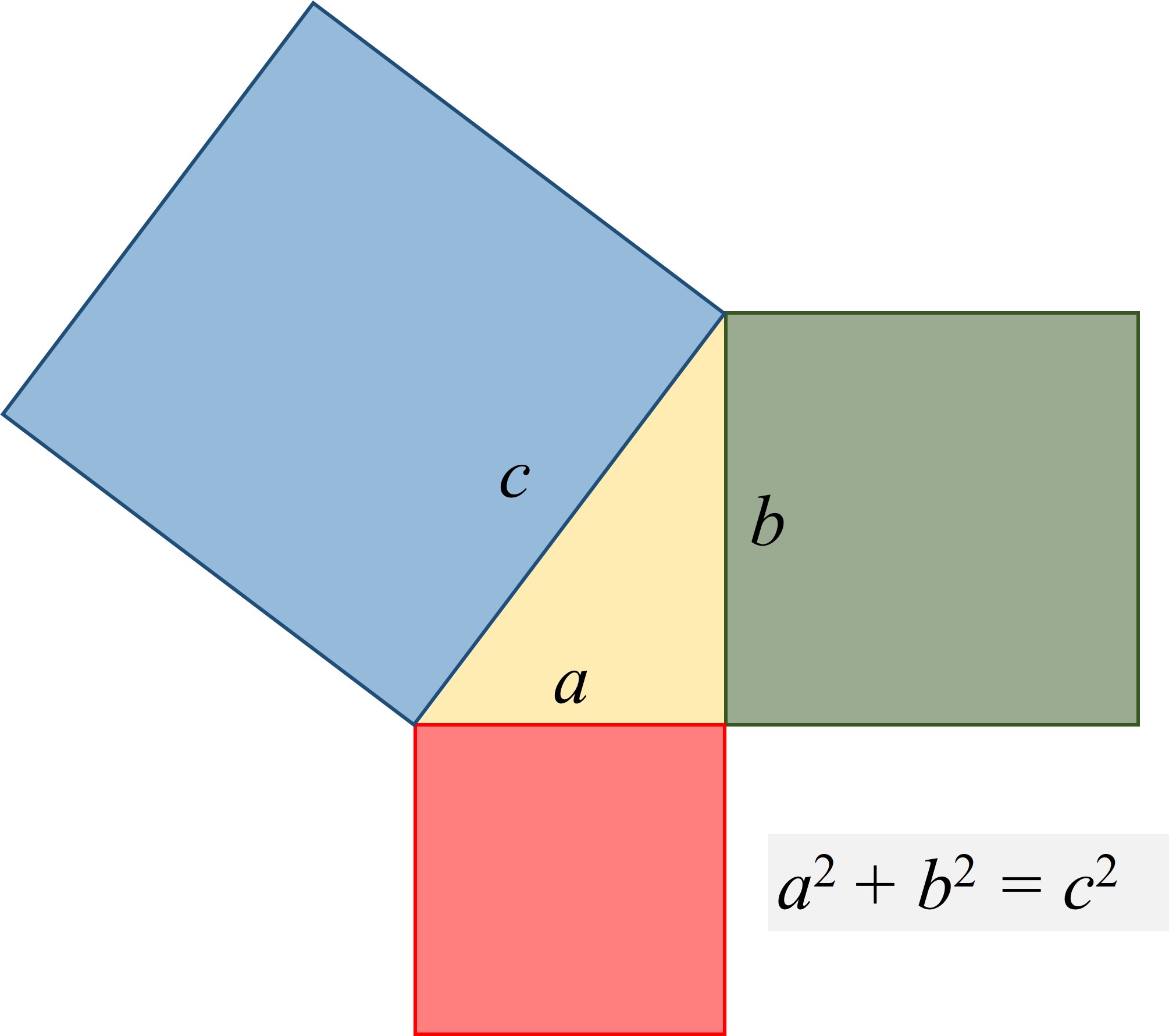
En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

¿Sabías que este teorema, llamado de PITÁGORAS, era conocido desde mucho antes?

• En Egipto: los egipcios utilizando unas cuerdas de 12 unidades realizaban ángulos rectos perfectos, construyendo un triángulo rectángulo de lados con longitudes de 3, 4 y 5 unidades.
  
  
• En Mesopotamia: la civilización sumeria escribía en tablillas de arcilla (escritura cuneiforme). Edgar Banks descubrió una tablilla cuneiforme, la llamada Plimpton 322, escrita entre los años 1822 y 1762 a.C. y en ella se ha descubierto que los babilonios usaban el célebre teorema de Pitágoras incluso más de mil años antes de que el propio Pitágoras (569-475 a. C.) hubiese nacido.
  
  
• En China: en el manuscrito chino "Chon Pei Suan O ching", traducido como "Aritmética Clásica de los Grados y de las Trayectorias Circulares del Cielo", se encuentra una descripción de un triángulo rectángulo con sus correspondientes relaciones. También en "Chiu Chang Shuan Shu", traducido como "Nueve Capítulos de Artes Matemáticas", aparece un problema que demuestra que los chinos conocían dicho resultado.
  
  
  
• En India: aparece mencionado en una estrofa de Baudhayana Sulbasutra, texto escrito por el matemático y religioso indio Baudhayāna.

Ejercicio 1:

• Investiga la forma de construcción de las pirámides en Egipto.
• Investiga sobre Edgar Banks y la tablilla Plimpton 322.
• Busca el enunciado en castellano del problema referido en "Nueve capítulos de Artes Matemáticas" y resuélvelo.
• Lee con atención más información sobre el teorema de Pitágoras y otros resultados matemáticos de Baudhayāna, matemático de la antigua India en
  
  https://factslegend.org/indian-mathematician-baudhayana-originally-discovered-pythagorean-theorem/ (Está en inglés)

Teorema recíproco del teorema de Pitágoras

Si en un triángulo el cuadrado del lado mayor es igual a la suma de los cuadrados de los otros dos lados ENTONCES dicho triángulo es rectángulo.

Y aún más, podemos saber si un triángulo de lados a < b < c es rectángulo, acutángulo u obtusángulo:

• Si a² + b² = c² ENTONCES el triángulo es rectángulo
• Si a² + b² > c² ENTONCES el triángulo es acutángulo 
• Si  a² + b² < c² ENTONCES el triángulo es obtusángulo

Ejercicio 2: Dibuja con regla y compás los siguiente triángulos (o usa GEOGEBRA) y determina comprobando las relaciones anteriores si son rectángulos, acutángulos u obtusángulos

• a = 3, b = 4 y c = 5
• a = 3, b = 4 y c = 4
• a = 3, b = 4 y c = 6

Por cierto, (3,4,5) recibe el nombre de TERNA PITAGÓRICA: números enteros positivos que verifican el teorema de Pitágoras, 3² + 4² = 5², o sea, son las longitudes de los lados de un triángulo rectángulo.

Ejercicio 3: ¿Existen más ternas pitagóricas? 

Ya sabemos que el teorema de Pitágoras tiene muchas DEMOSTRACIONES. Veamos una que es consecuencia del teorema de Tales (en Matemáticas un teorema que es consecuencia inmediata de otro se dice COROLARIO).

Pregunta: ¿Cuántos triángulos ves en la figura anterior? ¿Y cómo son? 
Respuesta: 3 y son todos RECTÁNGULOS. Y más aún, son SEMEJANTES.

Por el teorema de los catetos (consecuencia de dicha semejanza): 

• b² = ma
• c² = na

Por tanto, b² + c² = ma + na = (m+n)a = aa = a²

Ejercicio 4: Comprende los ejercicios resueltos de las páginas 144 y 145 del libro de texto y realiza los ejercicios de la página 145.