Esta publicación es para los alumnos de
Matemáticas Aplicadas a las Ciencias Sociales
Gracias a
|
Hemos empezado este tema con un juego de azar
“Dos contendientes, A y B, se juegan 3 000 doblones (han puesto 1 500 cada uno) a un juego de azar. Se lleva el dinero quien gane tres partidas. Cuando A va ganando 2 a 0, hay que interrumpir el juego, sin posibilidad de reanudarlo después. ¿Cómo han de repartir los 3 000 doblones?”
Un juego de azar se construye sobre un experimento aleatorio
En este ejemplo podemos suponer que cada partida consiste en lanzar una moneda y observar la cara visible. Un jugador apuesta por 3 caras y el otro por 3 cruces. Por tanto el experimento aleatorio compuesto sobre el que se construye el juego de azar consiste en observar el número de caras tras la realización consecutiva del experimento simple "lanzar una moneda y observar la cara visible" y parar cuando el número de caras o el número de cruces es 3.
Espacio muestral y asignación de probabilidades: E = {"sacar 3 caras","sacar 3 cruces"}
Suceso elemental
|
Probabilidad
|
“Sacar 3 caras”
|
1/2
|
“Sacar 3 cruces”
|
1/2
|
Ejercicio 1: Una vez aprendidas las estrategias aditivas y multiplicativas del cálculo de probabilidades, halla la probabilidad de dichos sucesos elementales.
Una variable aleatoria es una aplicación que asocia un número real (también llamado valor) a cada caso posible (sucesos elementales) de un experimento aleatorio. Pero nos vamos a quedar con la variabilidad de los valores asociados que es lo que le da el nombre de VARIABLE y por tanto la denotaremos con X.
En nuestro ejemplo, el juego de azar consiste en la siguiente variable aleatoria que podemos llamar X:
Suceso
elemental
|
Número (dinero) X
|
“Sacar 3 caras”
|
+1500
(ducados)
|
“Sacar 3 cruces”
|
–1500
(ducados)
|
Distribución de probabilidad o también función de probabilidad de una variable aleatoria es la aplicación que asocia a cada valor de la variable aleatoria la correspondiente probabilidad que tiene el suceso elemental asociado. En nuestro ejemplo del juego de azar:
Número (dinero) X
|
Probabilidad P
|
+1500 (ducados) x1
|
p1 = 1/2
|
–1500 (ducados) x2
|
p2 = 1/2
|
Tipos de variables aleatorias
Dependiendo del "número" de valores que puede tomar una variable aleatoria, tenemos dos tipos:
- DISCRETAS: un "número finito o numerable" de valores. Lo que podemos entender como números enteros (por tanto, valores ordenados). Distribución de probabilidad de una variable aleatoria discreta X que toma n valores:Variable aleatoria XProbabilidad Px1p1x2p2……xn-1pn-1xnpn
Recuerda que pi≥0, i=1..n y p1 + p2 + ... + pn-1 + pn = ∑pi = 1
La tabla anterior (distribución de probabilidad) también se puede expresar asíp[X = xi] = pi i = 1 .. n
y entonces se dice función de probabilidad.
A la función de probabilidad acumulada F(xi) = p[X ≤ xi] se le dice función de distribución.
- CONTINUAS: un "número infinito no numerable" de valores. Lo que podemos entender como un intervalo de números reales, o incluso todo R.
Observación: una variable estadística (*) se puede convertir en un experimento aleatorio extrayendo al azar un individuo de la población e incluso en una variable aleatoria asociando a las cualidades (también se dicen atributos o categorías) o a los valores de la variable estadística un número.
(*) Ha llegado el momento de saber un poco de ESTADÍSTICA DESCRIPTIVA. Realiza una lectura comprensiva de los temas 14 y 15 del libro de texto. Haz los ejercicios y aquí tienes más ejercicios resueltos de Estadística Descriptiva en la web de la profesora Carmen (carmesi__@hotmail.com)
Ejercicio 2: En una población de 100 individuos consideramos la siguiente variable estadística cualitativa dicotómica: sexo (¿realmente es dicotómica?). En dicha población hay 23 mujeres, y se extrae al azar un individuo de dicha población. ¿Cuál es la probabilidad de que sea un hombre? Explicita la variable aleatoria y su distribución de probabilidad. ¿Tiene algún sentido asociar un número a una cualidad, atributo o categoría?
Recuerda que con los números podemos OPERAR y por ello podemos "resumir" una variable aleatoria con el cálculo de unos parámetros o medidas.
Parámetros de una variable aleatoria discreta X
Ejercicio 3: Un juego de azar con apuesta es una variable aleatoria. Consideramos el siguiente juego de azar: apostar un euro a que sale una pareja al lanzar dos dados y caso de ganar recibir 5 euros. Explicita la variable aleatoria y su distribución de probabilidad. Halla la esperanza matemática y la varianza. ¿Es un juego justo?
Ejercicio 4: Explicita la variable aleatoria y su distribución de probabilidad del juego de azar con apuesta de la histórica partida interrumpida. Halla la esperanza matemática y la varianza. ¿Es un juego justo?
Ejercicio 5: En el experimento aleatorio "lanzar 3 monedas y observar las caras visibles" consideramos la variable aleatoria X = "número de caras obtenidas". Halla la función de probabilidad, la esperanza matemática y la varianza de dicha variable aleatoria.
La anterior variable aleatoria es un ejemplo de variable aleatoria binomial. En general, observamos la realización de un suceso aleatorio A cuya probabilidad es p y que vamos a llamar éxito y su contrario Ac tendrá entonces una probabilidad 1 - p que también se denota por q (es decir q = 1 - p) y lo llamaremos fracaso. Hacemos n realizaciones de dicho experimento aleatorio y consideramos X = "número de éxitos". X se dice variable aleatoria binomial y la denotaremos por B(n,p). Los valores que puede tomar la variable aleatoria X son 0, 1, 2, ... n-1 y n.
Observación: la ocurrencia de éxito en cada realización es independiente de la ocurrencia de éxito en la realización anterior y la probabilidad es siempre p.
En el ejemplo del ejercicio 5 el suceso aleatorio "éxito" es "sacar cara" cuya probabilidad es p = 0'5 y el número de realizaciones es n = 3. Por tanto X = "número de caras obtenidas" es una variable aleatoria binomial B(3,0'5). En este caso los valores que puede tomar la variable aleatoria X son 0, 1, 2 y 3.
Cada valor de la variable aleatoria puede ser visto como un suceso aleatorio simple o compuesto de un experimento aleatorio compuesto cuya asignación de probabilidades se realiza mediante el correspondiente diagrama de árbol y posteriormente se trata de CONTAR el número de casos favorables de cada suceso aleatorio correspondiente a cada valor de la variable aleatoria y así obtener la correspondiente asignación de probabilidades, o lo que es lo mismo la distribución de probabilidad o función de probabilidad de la variable aleatoria binomial.
¡CONTAR ... UN PROBLEMA DE COMBINATORIA!

Sea p la probabilidad del suceso aleatorio C (éxito) y sea q la probabilidad de su contrario X (fracaso), como las realizaciones son independientes la asignación de probabilidades es:
Y por tanto,
PROBLEMA DE COMBINATORIA: ¿De cuántas formas podemos obtener k éxitos (que el número de éxitos sea k) al hacer n realizaciones que algunos también llaman pruebas? Obviamente el número de fracasos será n - k. Es un ejercicio de permutaciones con repetición.
Podemos obtener r éxitos de PRnr,n-r formas. En el caso del ejercicio 5:
Y la función de probabilidad de una variable aleatoria binomial X, B(n,p) es
 k = 0 .. n
k = 0 .. n
Observación: A esta variable aleatoria se la llama binomial porque aparecen los números binómicos.
Ejercicio 7: Asumimos que la probabilidad de que un alumno de primer año de Bachillerato repita curso es de 0.2. ¿Cuál es la probabilidad de que en un grupo de 20 alumnos elegidos al azar haya 4 alumnos repetidores?
Tres formas para calcular las probabilidades de una distribución binomial B(n,p):
Ejemplo: Sea la variable estadística continua X = "peso de las niñas recién nacidas de un determinado grupo en un determinado hospital".
Ejercicio 8: Calcula la media y la desviación típica de la variable estadística continua X.
Ejercicio 9: Sea X la variable aleatoria continua "extraer al azar una bebé de la población del ejercicio 8 y observar su peso". ¿Cuál es la probabilidad de que dicho peso esté comprendido entre 2,75 y 3,75 kg?
Observación: para realizar el ejercicio 8 puedes usar una calculadora científica en modo estadístico, por ejemplo, la calculadora Casio fx-82ES. Y para ello pulsa las teclas <Mode><2>.
Aprende a usar la calculadora Casio fx-82ES en modo estadístico:
El histograma de frecuencias (absolutas o relativas) de una variable estadística continua fue inventado por Karl Pearson. La idea es agrupar los valores de la variable en intervalos y sobre ellos dibujar rectángulos cuya área sea la frecuencia (absoluta o relativa). En la imagen puedes observar la tabla de frecuencias de la variable estadística continua X agrupada en intervalos de la misma amplitud y el correspondiente histograma de frecuencias relativas. Por tanto, el área de todos los rectángulos de un histograma de frecuencias relativas es 1. Si trazamos los segmentos al unir los puntos medios de los lados superiores de los rectángulos de un histograma obtenemos el polígono de frecuencias. El área encerrada entre el polígono de frecuencias y el eje horizontal también vale 1. Observa en la imagen una curva roja, ¿qué representa?
Si hacemos tender las amplitudes de los rectángulos del histograma a 0 entonces el polígono de frecuencias tiende a esa curva que representa la función de densidad de probabilidad o simplemente función de densidad
Hay muchos ejemplos de variables aleatorias CONTINUAS pero hay un tipo muy básico que vamos a estudiar: la variable aleatoria normal o variable aleatoria de Gauss.
Gauss y Laplace contribuyeron a encontrar que la función de densidad de una distribución normal de media μ y desviación típica σ es:
Ejercicio 10: Asumimos que la variable X del ejercicio anterior sigue una distribución normal de media y desviación típica las obtenidas en el ejercicio 8. ¿Cuál es la probabilidad de que el peso de una bebé extraída al azar esté comprendido entre 2,75 y 3,75 kg?
Observación 1: para calcular probabilidades de una distribución normal podemos usar la tabla de la distribución normal estándar, Z, la que tiene media 0 y desviación típica 1, N(0,1), que es la única que está tabulada con su función de distribución, F:
(*) Las tablas de las distribuciones binomial (función de probabilidad) y normal (función de distribución) más habituales (proporcionadas en un examen de la EBAU) son:
Observación: la tabla de la distribución normal estándar Z, N(0,1), tabula la función de distribución para valores no negativos.
Uso de la tabla de la distribución normal estándar N(0,1):
Proposición: X es N(μ,σ) si y sólo si Z es N(0,1)
También podrías usar una calculadora online:
Teorema de De Moivre:
(*) Ha llegado el momento de saber un poco de ESTADÍSTICA DESCRIPTIVA. Realiza una lectura comprensiva de los temas 14 y 15 del libro de texto. Haz los ejercicios y aquí tienes más ejercicios resueltos de Estadística Descriptiva en la web de la profesora Carmen (carmesi__@hotmail.com)
Ejercicio 2: En una población de 100 individuos consideramos la siguiente variable estadística cualitativa dicotómica: sexo (¿realmente es dicotómica?). En dicha población hay 23 mujeres, y se extrae al azar un individuo de dicha población. ¿Cuál es la probabilidad de que sea un hombre? Explicita la variable aleatoria y su distribución de probabilidad. ¿Tiene algún sentido asociar un número a una cualidad, atributo o categoría?
Recuerda que con los números podemos OPERAR y por ello podemos "resumir" una variable aleatoria con el cálculo de unos parámetros o medidas.
Parámetros de una variable aleatoria discreta X
- Media o valor esperado o esperanza matemática: E[X] = ∑xipi
- Varianza: V[X] = ∑xi2pi-E[x]2 Desviación típica: σX = √V[X]
Ejercicio 3: Un juego de azar con apuesta es una variable aleatoria. Consideramos el siguiente juego de azar: apostar un euro a que sale una pareja al lanzar dos dados y caso de ganar recibir 5 euros. Explicita la variable aleatoria y su distribución de probabilidad. Halla la esperanza matemática y la varianza. ¿Es un juego justo?
Ejercicio 4: Explicita la variable aleatoria y su distribución de probabilidad del juego de azar con apuesta de la histórica partida interrumpida. Halla la esperanza matemática y la varianza. ¿Es un juego justo?
Variable aleatoria o distribución binomial
Las variables aleatorias de los ejercicios anteriores son DISCRETAS. Hay muchos ejemplos más pero hay un tipo muy básico que vamos a estudiar: la variable aleatoria binomial.Ejercicio 5: En el experimento aleatorio "lanzar 3 monedas y observar las caras visibles" consideramos la variable aleatoria X = "número de caras obtenidas". Halla la función de probabilidad, la esperanza matemática y la varianza de dicha variable aleatoria.
La anterior variable aleatoria es un ejemplo de variable aleatoria binomial. En general, observamos la realización de un suceso aleatorio A cuya probabilidad es p y que vamos a llamar éxito y su contrario Ac tendrá entonces una probabilidad 1 - p que también se denota por q (es decir q = 1 - p) y lo llamaremos fracaso. Hacemos n realizaciones de dicho experimento aleatorio y consideramos X = "número de éxitos". X se dice variable aleatoria binomial y la denotaremos por B(n,p). Los valores que puede tomar la variable aleatoria X son 0, 1, 2, ... n-1 y n.
Observación: la ocurrencia de éxito en cada realización es independiente de la ocurrencia de éxito en la realización anterior y la probabilidad es siempre p.
En el ejemplo del ejercicio 5 el suceso aleatorio "éxito" es "sacar cara" cuya probabilidad es p = 0'5 y el número de realizaciones es n = 3. Por tanto X = "número de caras obtenidas" es una variable aleatoria binomial B(3,0'5). En este caso los valores que puede tomar la variable aleatoria X son 0, 1, 2 y 3.
Cada valor de la variable aleatoria puede ser visto como un suceso aleatorio simple o compuesto de un experimento aleatorio compuesto cuya asignación de probabilidades se realiza mediante el correspondiente diagrama de árbol y posteriormente se trata de CONTAR el número de casos favorables de cada suceso aleatorio correspondiente a cada valor de la variable aleatoria y así obtener la correspondiente asignación de probabilidades, o lo que es lo mismo la distribución de probabilidad o función de probabilidad de la variable aleatoria binomial.
¡CONTAR ... UN PROBLEMA DE COMBINATORIA!
Sea p la probabilidad del suceso aleatorio C (éxito) y sea q la probabilidad de su contrario X (fracaso), como las realizaciones son independientes la asignación de probabilidades es:
Sucesos elementales
|
Probabilidad
|
CCC
|
p3
|
CCX
|
p2q
|
CXC
|
p2q
|
CXX
|
pq2
|
XCC
|
p2q
|
XCX
|
pq2
|
XXC
|
pq2
|
XXX
|
q3
|
Y por tanto,
Sucesos elementales
|
Variable aleatoria X
|
Probabilidad P
|
“Sacar 3 caras” = ¨{CCC}
|
3
|
p3
|
“Sacar 2 caras” = ¨{CCX, CXC, XCC}
|
2
|
p2q
+ p2q + p2q
|
“Sacar 1 cara” = ¨{CXX, XCX, XXC}
|
1
|
pq2+
pq2+ pq2
|
“Sacar 0 caras” = ¨{ XXX }
|
0
|
q3
|
PROBLEMA DE COMBINATORIA: ¿De cuántas formas podemos obtener k éxitos (que el número de éxitos sea k) al hacer n realizaciones que algunos también llaman pruebas? Obviamente el número de fracasos será n - k. Es un ejercicio de permutaciones con repetición.
Podemos obtener r éxitos de PRnr,n-r formas. En el caso del ejercicio 5:
- Podemos obtener 3 caras de PR33,0 = 1 forma
- Podemos obtener 2 caras de PR32,1 = 3 formas
- Podemos obtener 1 cara de PR31,2 = 3 formas
- Podemos obtener ninguna cara de PR30,3 = 1 forma
Por tanto la distribución de probabilidad o la función de probabilidad de dicha variable aleatoria binomial X, B(3,p) es (y en el caso particular de p = 1/2):
En Matemáticas hay diferentes maneras de resolver un mismo problema. Veamos otra manera de contar de cuántas formas podemos obtener k éxitos al hacer n realizaciones. Para comprenderlo mejor veamos antes un ejercicio de combinatoria.
Ejercicio 6 (resuelto): ¿Cuántos equipos de 6 titulares podemos formar con 12 jugadores de balonvolea? Tenemos 12 jugadores y los selecciono para ser titulares asignándoles una "T" de titular, no puedo dar dos "T" a un mismo jugador y el orden en que se colocan los 6 jugadores en dicho equipo titular no es relevante (es un solo equipo independientemente del orden en que se coloquen). Tenemos que hacer agrupaciones de 6 elementos en las que no importa el orden y no se puede repetir, por tanto, el número de formas posibles es combinaciones de 12 elementos tomados de 6 en 6 que se escribe C126 = V126 / P6 = (12 · 11 · 10 · 9 · 8 · 7) / (6 · 5 · 4 · 3 · 2 · 1) = 924.
Si eliminamos el contexto del ejercicio anterior y generalizamos el enunciado equivalente es: ¿cuántos subconjuntos de m elementos hay en un conjunto de n elementos? (m = 0 .. n). ¡Sí, hay un subconjunto con 0 elementos, llamado conjunto vacío!
Las combinaciones de n elementos tomados de m en m (m<n) Cnm se dicen números combinatorios y también números binómicos y en este caso se cambia la notación (*) porque aparecen en los coeficientes del desarrollo de la potencia n-ésima de un binomio, la conocida fórmula del binomio de Newton. Estos números combinatorios (o binómicos) también forman un conocido triángulo numérico llamado triángulo de Tartaglia o de Pascal.
(*) Notación de los números binómicos y fórmula del bimonio de Newton:
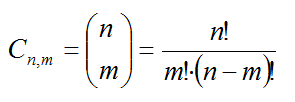
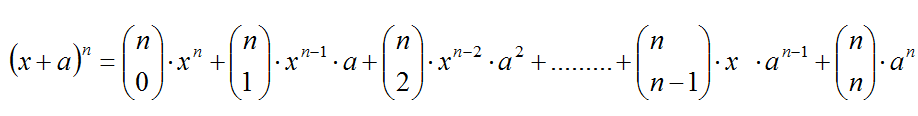
¿De cuántas formas podemos obtener k éxitos al hacer n realizaciones? Las n realizaciones son los n elementos del conjunto (jugadores de balonvolea) y tengo que asignarles los k éxitos "C" (elegir las k realizaciones con éxito), por tanto, las formas de obtener k éxitos al hacer n realizaciones son las combinaciones de n elementos tomados de k en k, Cnk.
En general, la distribución de probabilidad de una variable aleatoria binomial X, B(n,p) es:
Variable
aleatoria X
|
Probabilidad
P
|
Probabilidad
P
(cuando p = ½) |
3
|
1p3
|
1/8 = 0,1250 = 12,50%
|
2
|
3p2q
|
3/8 = 0,3750 = 37,50%
|
1
|
3pq2
|
3/8 = 0,3750 = 37,50%
|
0
|
1q3
|
1/8 = 0,1250 = 12,50%
|
En Matemáticas hay diferentes maneras de resolver un mismo problema. Veamos otra manera de contar de cuántas formas podemos obtener k éxitos al hacer n realizaciones. Para comprenderlo mejor veamos antes un ejercicio de combinatoria.
Ejercicio 6 (resuelto): ¿Cuántos equipos de 6 titulares podemos formar con 12 jugadores de balonvolea? Tenemos 12 jugadores y los selecciono para ser titulares asignándoles una "T" de titular, no puedo dar dos "T" a un mismo jugador y el orden en que se colocan los 6 jugadores en dicho equipo titular no es relevante (es un solo equipo independientemente del orden en que se coloquen). Tenemos que hacer agrupaciones de 6 elementos en las que no importa el orden y no se puede repetir, por tanto, el número de formas posibles es combinaciones de 12 elementos tomados de 6 en 6 que se escribe C126 = V126 / P6 = (12 · 11 · 10 · 9 · 8 · 7) / (6 · 5 · 4 · 3 · 2 · 1) = 924.
Si eliminamos el contexto del ejercicio anterior y generalizamos el enunciado equivalente es: ¿cuántos subconjuntos de m elementos hay en un conjunto de n elementos? (m = 0 .. n). ¡Sí, hay un subconjunto con 0 elementos, llamado conjunto vacío!
Las combinaciones de n elementos tomados de m en m (m<n) Cnm se dicen números combinatorios y también números binómicos y en este caso se cambia la notación (*) porque aparecen en los coeficientes del desarrollo de la potencia n-ésima de un binomio, la conocida fórmula del binomio de Newton. Estos números combinatorios (o binómicos) también forman un conocido triángulo numérico llamado triángulo de Tartaglia o de Pascal.
(*) Notación de los números binómicos y fórmula del bimonio de Newton:
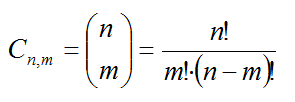
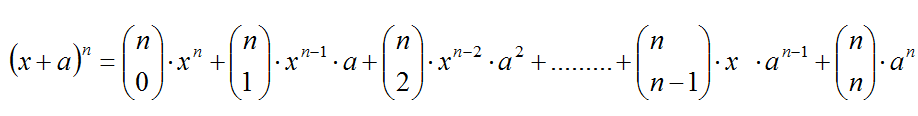
¿De cuántas formas podemos obtener k éxitos al hacer n realizaciones? Las n realizaciones son los n elementos del conjunto (jugadores de balonvolea) y tengo que asignarles los k éxitos "C" (elegir las k realizaciones con éxito), por tanto, las formas de obtener k éxitos al hacer n realizaciones son las combinaciones de n elementos tomados de k en k, Cnk.
En general, la distribución de probabilidad de una variable aleatoria binomial X, B(n,p) es:
Variable aleatoria X
|
Probabilidad P
|
0
|
Cn0qn
|
1
|
Cn1p1qn-1
|
2
|
Cn2p2qn-2
|
…
|
…
|
n - 1
|
Cnn-1pn-1q1
|
n
|
Cnnpn
|
Y la función de probabilidad de una variable aleatoria binomial X, B(n,p) es
 k = 0 .. n
k = 0 .. nObservación: A esta variable aleatoria se la llama binomial porque aparecen los números binómicos.
Ejercicio 7: Asumimos que la probabilidad de que un alumno de primer año de Bachillerato repita curso es de 0.2. ¿Cuál es la probabilidad de que en un grupo de 20 alumnos elegidos al azar haya 4 alumnos repetidores?
Tres formas para calcular las probabilidades de una distribución binomial B(n,p):
- La función de probabilidad y una calculadora.
- Las tablas de la distribución binomial (funciones de probabilidad y de distribución).
- La aproximación mediante una distribución normal (teorema de De Moivre).
Parámetros de una variable aleatoria binomial X B(n,p)
- Esperanza matemática: E[X] = ∑xipi = ... = np
- Varianza: V[X] = ∑xi2pi-E[x]2 = ... = npq
- Desviación típica: σX = √V[X] = √npq
Variables aleatorias continuas: distribución normal
Las variables aleatorias continuas están asociadas a variables estadísticas continuas.Ejemplo: Sea la variable estadística continua X = "peso de las niñas recién nacidas de un determinado grupo en un determinado hospital".
Ejercicio 8: Calcula la media y la desviación típica de la variable estadística continua X.
Ejercicio 9: Sea X la variable aleatoria continua "extraer al azar una bebé de la población del ejercicio 8 y observar su peso". ¿Cuál es la probabilidad de que dicho peso esté comprendido entre 2,75 y 3,75 kg?
Observación: para realizar el ejercicio 8 puedes usar una calculadora científica en modo estadístico, por ejemplo, la calculadora Casio fx-82ES. Y para ello pulsa las teclas <Mode><2>.
Aprende a usar la calculadora Casio fx-82ES en modo estadístico:
- http://diarioprofemates.blogspot.com/2019/06/calculadora-casio-fx82es.html
- https://www.edu-casio.es/recursos-didacticos/
- https://www.edu-casio.es/ebau-2020-se-puede-usar-calculadora-en-los-examenes-cual/
Si hacemos tender las amplitudes de los rectángulos del histograma a 0 entonces el polígono de frecuencias tiende a esa curva que representa la función de densidad de probabilidad o simplemente función de densidad
La función de densidad de probabilidad de una variable aleatoria continua o simplemente función de densidad es una función f con las siguientes propiedades:
- No negativa con dominio I un intervalo pudiendo ser R: f≥0.
- La integral definida de f en I (R) es 1 (área de la región limitada por la gráfica de f y el eje X).
La función de densidad de probabilidad nos va a dar la probabilidad de que los valores de la variable aleatoria continua estén comprendidos entre dos valores determinados a y b, es decir, p(a<X<b) = p(a<X≤b) = p(a≤X≤b) = p(a≤X<b) = área del recinto verde de la figura. Observa que es irrelevante incluir o no dichos valores a y b. Pues la probabilidad de que la variable tome un valor determinado es 0 (recuerda que es un área).
Gauss y Laplace contribuyeron a encontrar que la función de densidad de una distribución normal de media μ y desviación típica σ es:
En esta historia de la distribución normal también aparece un matemático estadounidense, Robert Adrain, al descubrir en 1808 la distribución normal de los errores de manera independiente a Gauss.
Observación 1: para calcular probabilidades de una distribución normal podemos usar la tabla de la distribución normal estándar, Z, la que tiene media 0 y desviación típica 1, N(0,1), que es la única que está tabulada con su función de distribución, F:
F(z) = p(Z≤z)
(*) Las tablas de las distribuciones binomial (función de probabilidad) y normal (función de distribución) más habituales (proporcionadas en un examen de la EBAU) son:
Observación: la tabla de la distribución normal estándar Z, N(0,1), tabula la función de distribución para valores no negativos.
- https://youtu.be/my5lmXgQcjg
- https://youtu.be/xZNvslIyRTk
- https://youtu.be/fWDGC1kTakk
- https://youtu.be/xJnC1Vj5KJo
- https://youtu.be/wD2BnCKC0nE
Observación 2: Antes de realizar el ejercicio 10 necesitarás tipificar la variable pues la variable aleatoria X sigue una distribución normal N(μ,σ) con una media μ y una desviación típica σ. Tipificar la variable significa hacer el siguiente cambio de variable:
Z = (X - μ) / σ
Proposición: X es N(μ,σ) si y sólo si Z es N(0,1)
También podrías usar una calculadora online:
- Geogebra: http://docentes.educacion.navarra.es/msadaall/geogebra/figuras/normal5b.html
- Wolfram Alpha: https://www.wolframalpha.com/widgets/view.jsp?id=9203ba181875bdf1a47f41be632e945a
- Calcme: https://docs.wiris.com/es/calc/menu#ex.normal
- Rossman: http://www.rossmanchance.com/applets/NormCalc.html
Teorema de De Moivre:

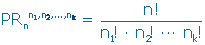






No hay comentarios:
Publicar un comentario